1. What is the scheduling problem with energy storage?
Energy storage plays a crucial role in smart grids, enabling more efficient power management and supporting the integration of renewable energy sources. When energy storage systems are included in economic dispatch, the scheduling problem becomes more complex. This type of problem can typically be modeled mathematically, as shown in Figure 1 (assuming that the charge and discharge prices are given parameters). The goal is to minimize the total operating cost of the grid under various constraints, such as energy storage operation limits, unit generation constraints, and network flow restrictions. With the inclusion of energy storage, two additional cost components must be considered: the cost of charging the storage system and the cost of discharging it.
2. How do the charge and discharge costs work?
The charging cost depends on whether the price is positive or negative. If the charge price is positive, the energy storage pays the grid for the electricity it charges. Conversely, if the charge price is negative, the grid compensates the storage for the energy it receives. Similarly, for the discharge cost, if the discharge price is positive, the grid pays the storage for the energy it uses. If the price is negative, the storage has to pay the grid for the energy it releases.
3. What happens when there’s a long-term contract?
If an energy storage system has a long-term agreement with the grid, its operational cost may not be directly included in the dispatch process. In this case, the charge and discharge prices can be set to zero, simplifying the model significantly.
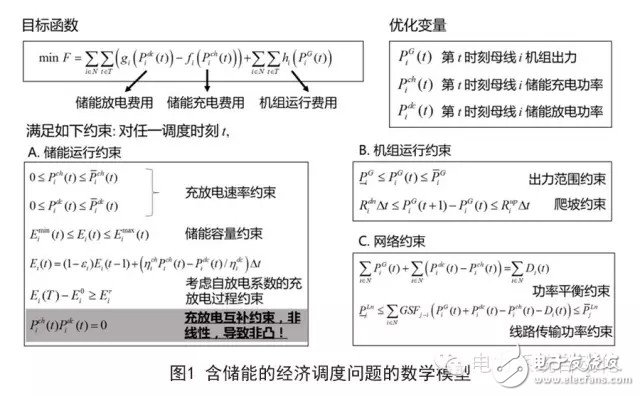
4. What are the main challenges in energy storage scheduling?
One of the key challenges in scheduling with energy storage is the fact that a storage system cannot charge and discharge simultaneously. This constraint must be incorporated into the optimization model. A common approach is to use separate variables for charging and discharging power. However, this introduces a "complementary constraint," meaning that at any given time, either the charging power or the discharging power must be zero. This nonlinear constraint makes the optimization problem non-convex and difficult to solve efficiently.
5. How can we handle this challenge?
Instead of enforcing the complementary constraint directly, one possible solution is to relax it. This means removing the constraint from the model and solving a simpler version of the problem. The question then becomes: under what conditions will the relaxed solution still satisfy the original constraint? If such conditions exist, the complexity of the problem can be reduced significantly, leading to faster and more efficient solutions.
6. What conditions allow for a strict relaxation?
Strict relaxation is possible if two conditions are met simultaneously. First, the discharge price must always be higher than or equal to the charge price. Second, the charge price must not exceed the node price during any scheduling period. These conditions ensure that simultaneous charging and discharging is economically inefficient, making it unnecessary to enforce the complementary constraint explicitly.
7. How can we verify these conditions?
Condition 1 can be checked easily since the charge and discharge prices are inputs to the model. For Condition 2, historical data on node prices can be used to predict future values. If the predicted node price range is known, and the charge price falls below the minimum of that range, Condition 2 is satisfied.
8. Are these conditions generally valid?
In many real-world scenarios, especially in well-regulated markets, these conditions are often met. This means that in practice, the relaxed model can provide accurate results without violating the complementary constraint, significantly improving computational efficiency and making large-scale scheduling more feasible.
A phone charger is a device used to charge a mobile phone or smartphone. It typically consists of a power adapter that plugs into a wall outlet and a cable that connects to the phone's charging port. The charger converts the electrical current from the wall outlet into a suitable voltage and amperage to charge the phone's battery.
Phone Charger,phone charger fast charging,Car Charger Adapter for Wall Plug,mobile phone chargers
Pogo Technology International Ltd , https://www.wisesir.net