Summary
This article is based on the traditional non-isolated solution of the LM3445, which explains how it works. We will derive and analyze this linear regulation formula. The results of the calculations were verified by actual experimental results and proved to be very closely matched. In order to evaluate the feasibility of mass production, we thoroughly studied and analyzed the output current tolerance. The results prove that it is difficult for conventional solutions to achieve full mass production current tolerance, especially in the current trend of higher output applications required by the market.
To solve this problem, we recommend using a simple linear regulator compensation circuit. We validated this proposed solution from both theoretical and experimental measurements. The final total current tolerance required for actual mass production is analyzed based on the derived output current and linear regulation rate formula. Based on the results obtained, we have found that great progress has been made in meeting this practical requirement. Finally, the test results and calculation results are compared based on the prototype; they are proved to be very matched.
1 Introduction
As LED indoor lighting continues to grow, non-isolated solutions and isolated solutions are becoming more and more popular. In particular, high linearity regulated high PF and accurate constant current mode solutions have become the dominant solutions in the market. However, because the output voltage becomes higher and wider, the traditional LM3444/L3445 non-isolated applications cannot meet this margin requirement, further limiting the application of the LM3445/LM3445.
In view of the above problems, the main goal of this paper is the high output applications required for precise linear regulation. In this article, the general working principle is explained by some formulas in Chapter 2. Using these formulas, we can solve the final output current. In order to evaluate the results, Chapter 3 introduces a unified formula through which the output current is simplified. In addition, Chapter 3 further details the current margin analysis. Chapter 4 gives some examples of prototype-based design. The calculation results and simulation results are given and compared with the experimental results. Their match proved to be very good. However, after in-depth research, we found that it is still difficult to meet the current tolerance requirements for mass production.
To solve this problem, we propose a proposed compensation circuit in Chapter 5. This compensation circuit was verified by calculation and simulation experiments. Finally, experiments have shown that the circuit significantly improves linear regulation and current margin performance. With this circuit, improved linear regulation will be more competitive in practical applications, especially in LED R30/PAR30/A19/E27 LED lighting applications.
2. The principle of the traditional non-isolated LM3444/LM3445 solution
Figure 1 shows a traditional non-isolated solution for higher PF. In order to explain how it works, we define the parameters as follows:
• Vout: LED output voltage
• I: equivalent time value in a single time period
• Kfeed: input feed forward coefficient of AC voltage
• Rs: current sense resistor
• Rup:toff charging resistor
• Cchar: toff charging capacitor
• Vinmin: AC input voltage minimum
• Vinmax: AC input voltage maximum
• Vinac: AC input voltage
• _noimp: no improved linear regulator circuit function
• _imp: Improved linear regulator circuit function
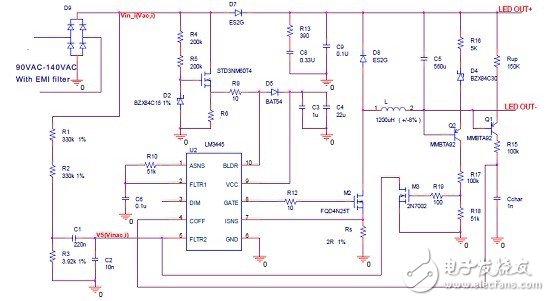
Figure 1 Traditional recommendations for high PF non-isolated solutions
This is a typical no feedback loop application, but it has the following features:
1, a higher PF. It is realized by inputting a feedforward circuit.
2. Constant current. This is achieved by the LED output voltage detection toff circuit.
The AC input voltage can be expressed as follows:

As shown in Figure 1, C1 is greater than C2 in order to achieve a higher PF value, for example: C1/C2 = 220n/10n. The voltage at pin 5 of the LM3444 or LM3445 can be expressed as: 
The charging current of toff is: 
For actual calculations, Veb_Q1 can be selected as a reference design.
Therefore, toff can be written as: 
The frequency can be expressed as: 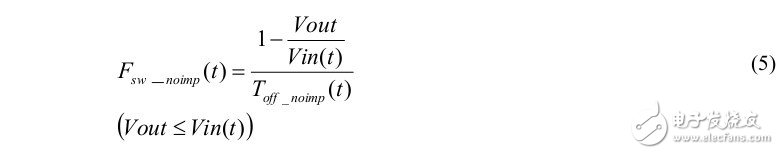
The ripple current of the inductor is: 
Therefore, the maximum current and average inductor current formula can be written as: 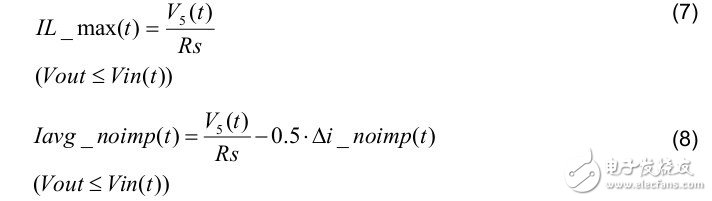
Then, the LED output current is: 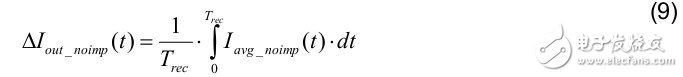
3. LED current linear voltage regulation analysis based on traditional solutions
Since the LED current has been derived above, we can write the general formula as: 
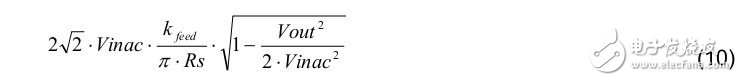
To derive the LED current variation for each input voltage, equation (10) can be simplified because Vout is generally less than Vinac and Vout is greater than Vbe_Q2. The formula can be simplified to: 
Then, the change in LED current over the entire input range can be derived using equation (11). 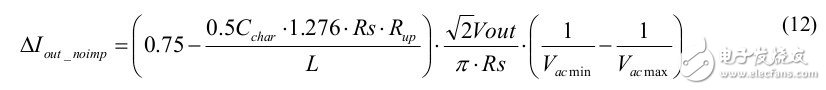
We can see that LED current variation is heavily dependent on Vout, which means it can use higher linear regulation when the LED voltage is lower, in which case it is well suited for GU10 applications.
3.1 Analysis of Δ LED current variation during mass production
Equation (11) derives the LED current variation, but this variation is affected by the Rs, L, Cchar, and Rup tolerances over the entire input range. According to the mass production requirements, we analyze it as follows:
1. The Δ LED current change during mass production is affected by Rs (for example: 2% tolerance) as follows:
2. The Δ LED current change during mass production is affected by Rup (for example: 2% tolerance) as follows: 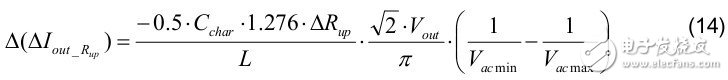
3. The Δ LED current change during mass production is affected by Cchar (for example: 10% tolerance) as follows: 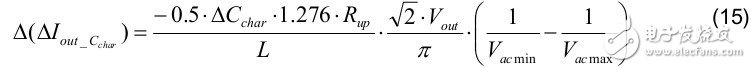
4. The Δ LED current change during mass production is affected by L (for example: 16% tolerance) as follows: 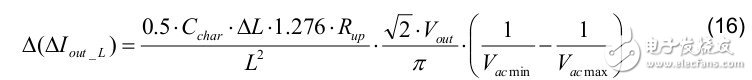
5. The extremes of Δ LED current change under a Vled in mass production are as follows: 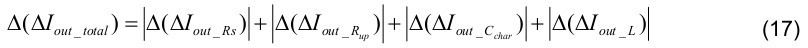
Under normal circumstances, this total change is very small compared to LED current changes.
3.2 LED current tolerance analysis during mass production
In mass production, LED current is regulated. Normally, it is required to be within ± 5%, which is independent of the tolerances of Vled, kfeed, L, Cchar, and Rup over the entire input range.
From equation (9), we know that LED current changes are affected by these parameters. The following is a detailed analysis.
1. The LED current variation during mass production is affected by Rs (for example: 2% tolerance) as follows: 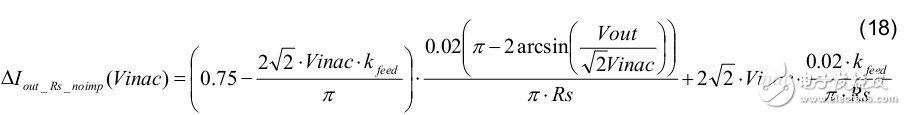
2. The LED current change during mass production is affected by Rup (for example: 2% tolerance) as follows: 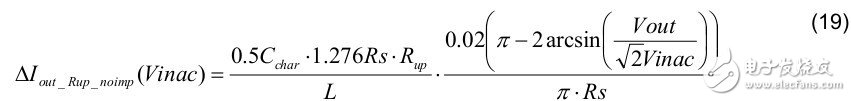
3. The LED current change during mass production is affected by Cchar (for example: 10% tolerance) as follows: 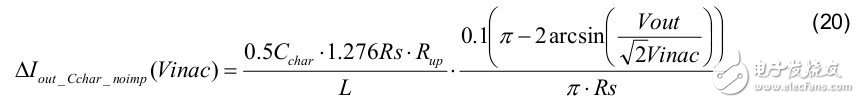
4. The total LED current variation during mass production is affected by L (for example: 16% tolerance) as follows:
5. The total LED current variation during mass production is affected by kfeed (for example: 2% tolerance) as follows: 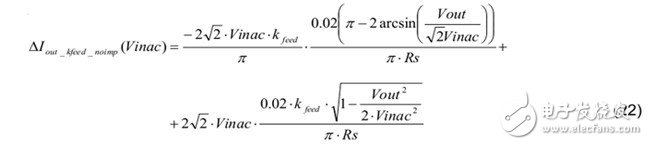
6. The extreme LED current changes under a certain Vled in mass production are as follows: 
Then, according to the mass production requirements, the total LED current tolerance can be expressed as: 
4 Example of linear regulator and mass production current tolerance design based on traditional solutions
In order to verify the validity of the above deduced calculation results, we made a prototype according to the parameters listed in Table 1.

Table 1 prototype parameters
Using the formula (5) in Chapter 2, the frequency plot shown in Figure 2 is obtained:
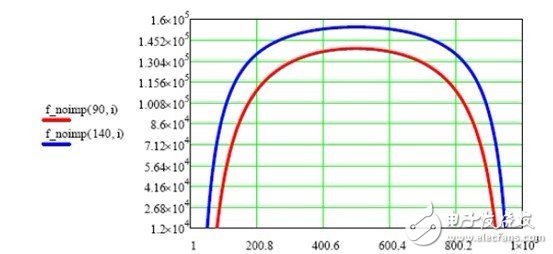
Figure 2 No improved solution frequency less than 90Vac and 140Vac
Using the equations (7) and (8) of Chapter 2, the maximum current and average current of the inductor are obtained (see Figure 3):
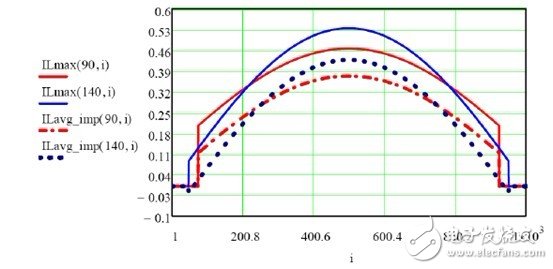
Figure 3. No improved solution output current for less than 90Vac and 140Vac
Figures 4 and 5 show simulation and experimental results for less than 90 Vac and 140 Vac.
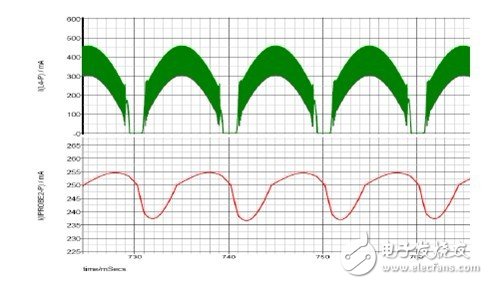
Figure 4 Simulation results of inductor current and output current below 90Vac 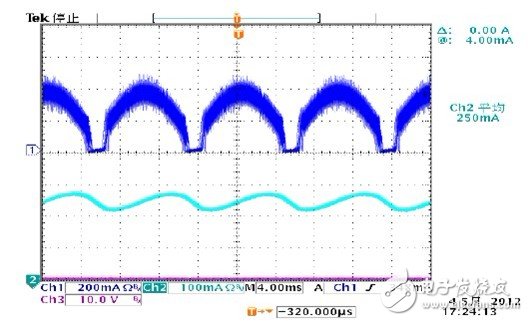
Figure 5 Test results of inductor current and output current below 90Vac
The measured and simulated current waveforms (see Figures 4 and 5) are almost identical; the output ripple indicates some small differences due to the difference between the LED simulation model and the actual test LED load.
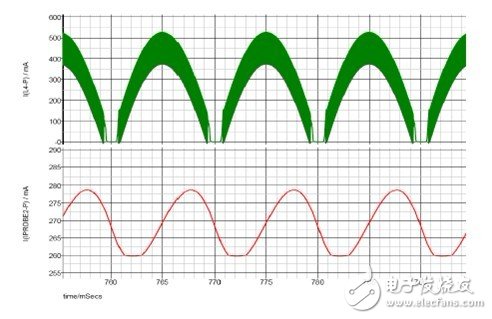
Figure 6 Simulation results of inductor current and output current below 140Vac 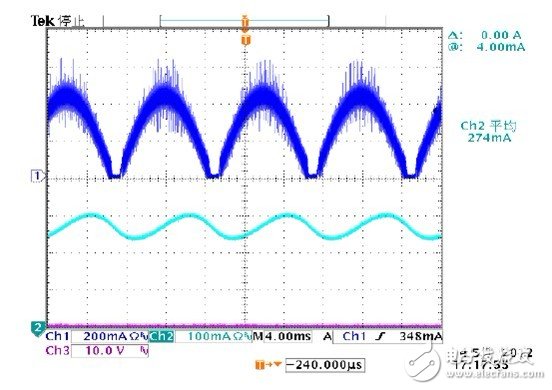
Figure 7 Test results of inductor current and output current below 140Vac
From the results shown in Fig. 6 and Fig. 7, the calculation results seem to closely match the simulation results with the actual measurement results. This result provides a strong theoretical support for the later tolerance analysis.
Use the formula 9 in Chapter 2 to calculate the standard output current; obtain the maximum and minimum output currents in the case of parameter tolerances during mass production:
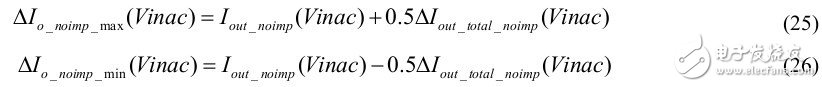
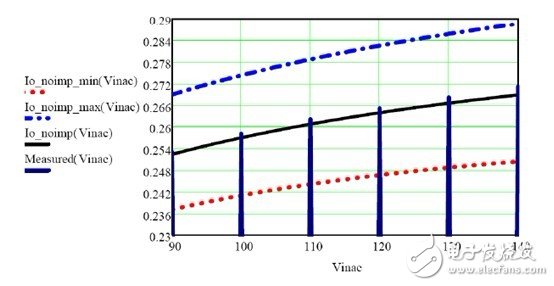
Figure 8 Output current without improved solution below 90Vac and 140 Vac
Using Equation (23) of Section 3.2, extreme LED current variations during mass production taking into account parameter tolerances are obtained.
Figure 9: No effect of component tolerance on LED output current changes from 90Vac to 140Vac
Use the formula (24) in section 3.2 to get the total LED current tolerance during mass production (see Figure 10):
Figure 10 Total LED Current Tolerance without Improved Solution from 90Vac to 140Vac in Mass Production
From equation (24), we can see that the normal LED current variation from 90Vac to above 140Vac is 17mA and the linear regulation is ±3.3%, which is acceptable for individual components. However, the main problem with actual engineering is the total adjustment feasibility, which is to consider the total LED current tolerance for component tolerances. From Figure 8, we know that the output current affected by component tolerance varies by approximately 32 mA. Therefore, the total LED current tolerance during mass production is ± 8% or more, as shown in Figure 10. This is also difficult to achieve in the actual production process. From the above analysis we can see that linear regulation is the key to improving the total tolerance of the input range.
5 Improved non-isolated LM3444/LM3445 solution works
In order to improve the linear regulation, we recommend using the line voltage compensation shown in Figure 11.
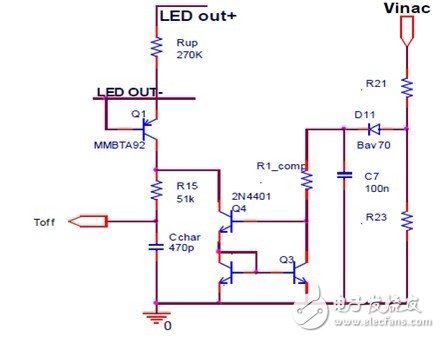
Figure 11 Improved line voltage compensation circuit
In order to reduce the latch current tolerance of the circuit shown in Fig. 11, higher precision resistors R21, R23 and R1_comp can be used. In order to reduce the forward voltage effects of D11, Q3 and Q4, we recommend that the C7 voltage be slightly higher (eg 20Vdc). In order to know the current tolerance at different temperatures, V_C7 is specified as 20V, Q4's V_c is 20V, and R_comp is 300K, and then SPICE temperature scanning simulation is performed. The result is shown in FIG.
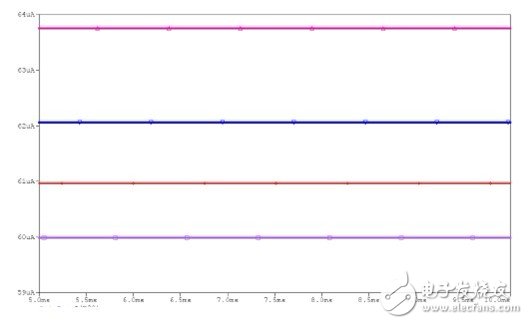
Figure 12 Scanning simulation results at 0 °C, 25 °C, 50 °C and 85 °C
From this result, we know that the temperature tolerance is ±3%, so we can enter the actual design.
After installing the compensation circuit (see Figure 11), the improved toff charging current is: 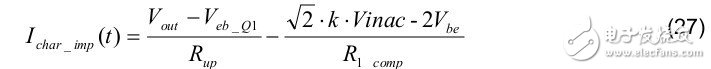
To reduce the effects of Vbe on Q3 and Q4 (as shown in Figure 11), we recommend that the factor k of equation (27) be as large as possible so that we can ignore Vbe in the design.
The maximum current and average inductor current equations are the same as equations (7) and (8) in Chapter 2. The final LED current formula is as follows:
If other component tolerances are not considered, the normalized formula for the output LED current can be written as: 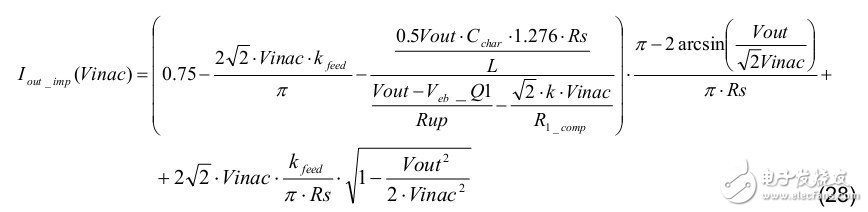
In the actual calculation process, we can make the following provisions: 0.95Char, 0.99Rs, 0.99Rup, 1.08L and 0.99 kfeed to get the maximum LED output current. The calculation formula is as follows: 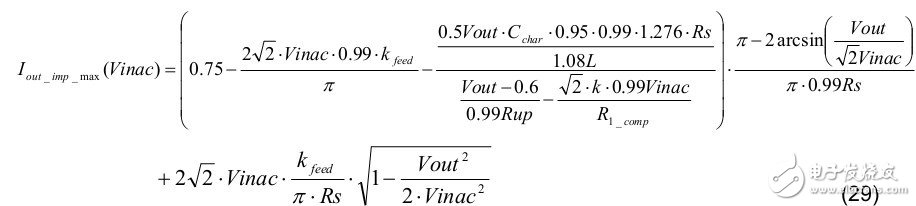
Using the same analysis, we can make the following rules: 1.05 Char, 1.01Rs, 1.01 Rup, 0.92 L, and 1.01 kfeed to get the minimum LED output current. The calculation formula is as follows: 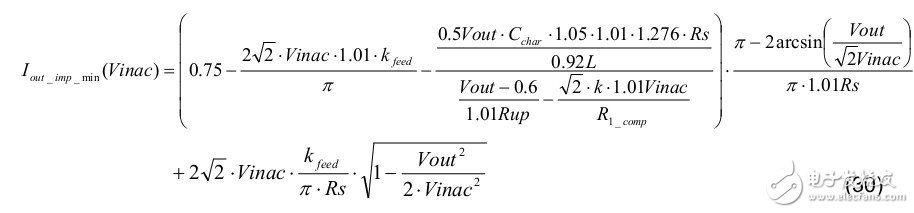
Then, we can get the following frequency range and the calculation method of the inductor current waveform.

Figure 13 Frequency below 90Vac and 140Vac 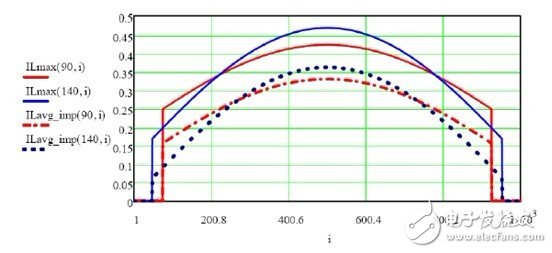
Figure 14 Inductor current below 90Vac and 140Vac
Figure 15 and Figure 16 show the results of the following 90Vac and 140Vac experiments.
Figure 15 Test results of inductor current and output current below 90Vac 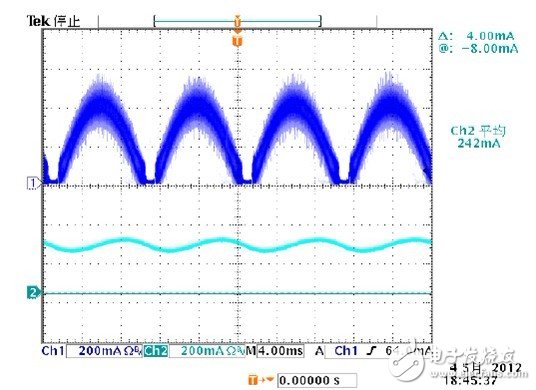
Figure 16 Inductor current and output current test results below 140Vac
Figure 17 shows the results of the linear regulation calculation:

Figure 17 Linear regulator calculation improved to less than ±1%
The output current is a non-linear curve of the input voltage, while the nonlinear curve. The compensation parameters greatly affect this curve. In the actual design, the engineer can optimize this curve by adjusting the line pressure compensation parameters.
In order to verify the result, the measurement results shown in Fig. 18 were compared with the calculated results.
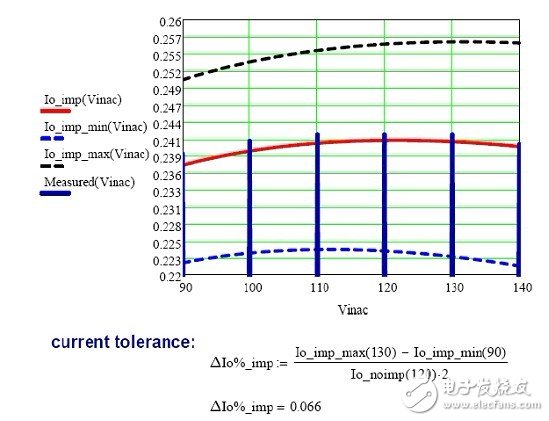
Figure 18 Extreme current tolerance calculation improved to ±6.6%
From Figure 18, we can see that the extreme current tolerance is also improved due to the use of an improved linear regulator circuit. In order to achieve this very extreme extreme current tolerance, our solution must be further refined to suit the needs of some special users.
If you consider the current tolerance below 90Vac, you can get:
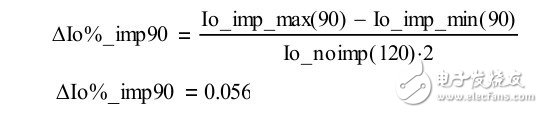
This can be achieved if the tolerances above 90 Vac are substantially the same; therefore, Figure 19 shows an alternative suggested approach.
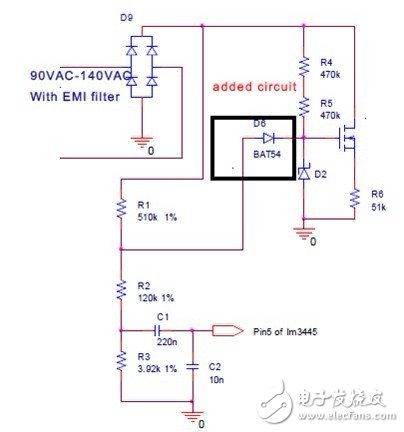
Figure 19 Linear regulator improvement circuit below 120Vac to 140Vac
The pin 5 voltage calculation method of LM3445/LM3444 is shown in Figure 20 and Figure 21:
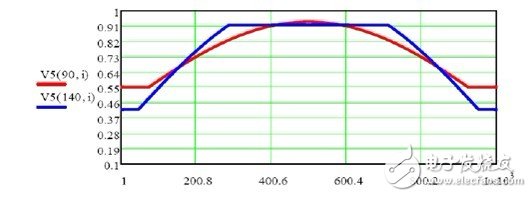
Figure 20 LM3445/LM3444 pin 5 voltage when adding the circuit of Figure 20. 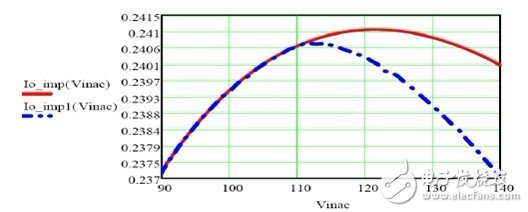
Figure 21 shows a significant improvement in linear regulation after using the circuit of Figure 19.
From the previous analysis, we can conclude that this circuit can help improve linear regulation. However, if the current tolerance of the line voltage compensation circuit is used to meet mass production requirements, this additional diode circuit cannot be used. However, if there is extra space in the PCB layout, TI still recommends using this additional diode circuit in the actual design.
Finally, Figure 22 shows a complete improvement solution for the alternative method.
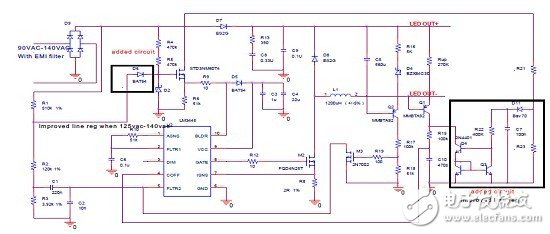
Figure 22 Alternative solution to dramatically improve linear regulation
in conclusion
Based on the traditional non-isolated LM3444/LM3445, this paper thoroughly analyzes the output current linear regulation and current tolerance. The result is that linear regulation is not ideal. To solve this problem, we propose an improved solution. In addition, we also describe linear regulation and total current tolerance. We demonstrate the feasibility of this solution through theoretical analysis and practical experiments.
Led Work Light is perfect for the home workshop or the work site. Operates on standard 120-volt household current. Stand adjusts from 2 feet to 6 feet in height. Safety wire guard, durable steel with powder coat finish fixture, and yellow color for safety.
Bbier equipped LED Work Light Tripod with 2 LED lights. Work Lamp are equivalent in output to 2 higher wattage halogen bulbs. 150 Watt Equivalent Led Bulb feature a lightweight, yet sturdy steel stand. You can adjust the stand to your desired height. All of these features provide Led Work Light Tripod with a life expectancy of 50,000 hours. LED Work Light Tripod provides ample lighting with its long-lasting LED bulb. Once detached from the tripod, its easy grip handle also allows it to be transported with ease.

LED Work Light Tripod
Led Work Light Tripod,150 Watt Equivalent Led Bulb,Work Lamp, Led Work Light
Shenzhen Bbier Lighting Co., Ltd , https://www.chinabbier.com